DÉMONSTRATION (THÉORIE DE LA)

DÉMONSTRATION (THÉORIE DE LA)

La théorie de la démonstration est la logique de la logique. En contraste avec d’autres sous-domaines tels que la théorie des modèles, les grandes questions qui ont tant passionné nos pères ont laissé une trace vivace dans cette discipline, qui s’occupe essentiellement (c’est là la définition technique de la théorie de la démonstration) de l’aspect syntaxique de la logique. Au début, grâce au programme de Hilbert, la théorie de la démonstration avait des visées claires et nettes; mais, après l’échec du programme (1931), tout devint beaucoup moins simple. En particulier, plus question de répondre de manière simpliste aux grandes interrogations ontologiques sur la nature des mathématiques... Faute de pierre philosophale, la discipline aurait pu disparaître; s’il n’en a rien été, c’est sans doute que l’étude générale des relations des objets finis aux objets infinis:

– dans la dénotation d’objets (infinis) par des constructions syntaxiques (finies),

– dans les preuves de propriétés d’objets (infinis) au moyen de démonstrations (finies),

constitue, par-delà les querelles d’école et les tentatives éphémères du genre de celle que fit Hilbert, le véritable objet de la théorie.

Les avancées en théorie de la démonstration semblent liées à un progrès quant aux méthodes utilisées, plus précisément quant à leur complexité logique :

– Hilbert tenta d’élaborer une théorie élémentaire de la démonstration («élémentaire» signifiant: de complexité logique nulle, cf. chap. 1);

– Gentzen a introduit les méthodes essentielles pour l’analyse des systèmes logiques finis (complexité logique ⁰¹, cf. chap. 2);

– plus tard, on a considéré des logiques généralisées (infinies); la plus connue d’entre elles est la logique avec 諸-règle (complexité logique 刺¹¹, cf. chap. 3); mais de nouvelles logiques de plus grande complexité ( 刺¹², voire 刺¹ⁿ : cf. chap. 4) sont maintenant utilisées de manière intensive.

Cette question de complexité logique fait l’objet de nombreux contresens; aussi importe-t-il de dire bien clairement en quoi elle intervient:

– individuellement, les objets considérés sont effectivement calculables , ils sont en pratique récursifs; il en est de même des opérations définies sur ces objets; par exemple les 諸-démonstrations sont toujours récursives et peuvent être normalisées (par élimination des coupures) effectivement. On voit donc que, pour les objets, la complexité logique ne joue pas;

– par contre, l’ensemble de tous les objets du genre considéré est logiquement complexe (l’ensemble des 諸-démonstrations récursives est 刺¹¹; cette complexité logique intervient de manière décisive dans la démonstration du théorème d’élimination des coupures, à savoir que la fonction effective qui élimine les coupures remplit bien son rôle);

– dans la pratique, la complexité logique joue surtout un double rôle; elle a un rôle «hygiénique»: assurer que tout se passe bien, que les opérations définies ont les propriétés attendues; elle joue aussi un rôle de révélateur: voir des problèmes simples de manière inhabituelle; le détour par des problèmes de très grande complexité logique peut permettre d’y voir clair dans des situations élémentaires embrouillées.

Une dernière mise en garde: ne pas croire que la complexité logique d’un problème soit un gage de profondeur...

1. Le programme de Hilbert

David Hilbert a proposé un programme de démonstration d’une opinion philosophique: le formalisme . La prétention de Hilbert à démontrer son point de vue a pour contrepartie évidente la possibilité de le réfuter; la philosophie s’accommode rarement de conclusions aussi tranchées! Même réfuté, le formalisme garde ses adeptes, notamment en France, avec Bourbaki: on sait bien que les idéologies simplistes ont un pouvoir d’attraction qui persiste même après leur échec patent; la réfutation de Hilbert par Gödel ne nous propose en aucune manière une vision de même nature: Gödel a détruit l’espoir de donner une réponse claire et nette à certaines interrogations essentielles, mais il n’a pas donné les bases d’un nouveau credo. Les mathématiques doivent être analysées comme une activité sans signification , semblable à un jeu , tel le jeu d’échecs: il s’agit de règles formelles fixées à l’avance et permettant de construire certains assemblages de symboles , à savoir les énoncés mathématiques et leurs démonstrations .

Voilà le credo formaliste; évidemment cette attitude s’accommode de positions ontologiques variées, depuis le solipsisme jusqu’aux différentes variantes de positivisme. L’élément essentiel de la pensée de Hilbert (et celle de son époque, le début du XX^e siècle), c’est peut-être le mécanisme : à l’opposé des intuitionnistes, qui, avec Brouwer, allaient proclamer le rôle essentiel du mathématicien en tant que sujet pensant , Hilbert réduit celui-ci à la dimension d’un robot: le sens des mathématiques, l’«intuition», ce n’est que ce qui permet de compenser en partie notre infériorité par rapport aux vraies machines.

L’ontologie hilbertienne est non vide: pour Hilbert, il y a certains objets, certaines propriétés, certaines démonstrations qui ont vraiment un sens, qui existent; il les appelle élémentaires : ce sont les entiers naturels (plus généralement, les constructions finies) pour ce qui est des objets; les propriétés élémentaires au sens de Hilbert, ce sont les énoncés de la forme: face=F0019 葉x ¹ ... 葉x ⁿ , f (x ¹, ..., x ⁿ ) = 0, où f est une fonction calculable, c’est-à-dire récursive. Les énoncés de cette forme sont dits 刺⁰¹, leurs négations ⁰¹; de très nombreux énoncés mathématiques ont cette forme ou s’y ramènent, citons pêle-mêle: le théorème de Fermat, la conjecture de Riemann, la conjecture de Goldbach, le théorème des quatre carrés, le problème des quatre couleurs... Quant aux démonstrations élémentaires, il s’agit évidemment de démonstrations n’utilisant que des énoncés élémentaires et des principes particulièrement immédiats de démonstration, comme l’induction (la récurrence) sur des énoncés élémentaires. Tout ce qui ne fait pas partie de l’élémentarité, Hilbert l’appelle abstrait (qu’il s’agisse d’objets, de propriétés ou de prédicats): pour lui, ces objets idéaux ne sont que des abstractions commodes permettant à la mauvaise machine qu’est le mathématicien de fonctionner plus efficacement; mais ces objets n’ont pas de sens en eux-mêmes. Le programme de Hilbert est une tentative pour démontrer la justesse de l’ontologie hilbertienne:

Étant donné une démonstration D d’un énoncé élémentaire R par des méthodes abstraites (par exemple , à l’aide de l’axiome du choix en théorie des ensembles ) montrer que R peut être obtenu directement dans les mathématiques élémentaires .

De plus, si l’on veut que le résultat ait une quelconque valeur épistémologique, le programme doit être montré par des méthodes élémentaires.

Le programme de Hilbert s’appuyait sur une certaine pratique mathématique: par exemple, le théorème des nombres premiers (Hadamard, La Vallée-Poussin) fut d’abord démontré par la théorie des fonctions analytiques; mais, plus tard, des démonstrations élémentaires furent données. Un principe «esthétique» de mathématiques est le principe de pureté des méthodes, qui consiste à ne pas utiliser de notions étrangères à l’énoncé démontré, et on voit bien que le programme de Hilbert est un principe général de pureté des méthodes. L’exemple de la théorie des corps réels clos (cf. théorie des MODÈLES) donne un exemple d’une situation analogue, où la pureté des méthodes est vraie.

Une variante du programme de Hilbert est la recherche de démonstrations de cohérence élémentaire . Il est d’ailleurs facile de voir que cette variante du programme de Hilbert est strictement équivalente à l’original.

Le premier théorème d’incomplétude de Gödel (1931) est un coup d’arrêt brutal et définitif au programme: l’énoncé de Gödel est élémentaire, vrai (on le sait par des méthodes non élémentaires), mais non prouvable dans la théorie elle-même: il suffit d’appliquer ce résultat à la formalisation des mathématiques élémentaires pour réfuter le programme de Hilbert. Quant au second théorème d’incomplétude, il réfute le programme sous sa forme de «démonstration de cohérence».

À l’époque où certains allaient bientôt mettre «mathématiques» au singulier (sous-entendu: la leur), ces résultats pourtant exceptionnellement clairs et définitifs n’allaient influencer de manière significative ni la pratique, ni la «philosophie» des mathématiciens. Paradoxalement, le succès des théorèmes d’incomplétude en dehors des milieux mathématiques n’a d’égal que l’incompréhension à peu près générale du résultat.

Rappelons que le théorème ne dit pas qu’une théorie ne peut pas se penser elle-même (non seulement les théories peuvent se penser elles-mêmes, c’est-à-dire exprimer les propriétés qui parlent d’elles-mêmes; mais, pour ce qui est de la plupart de ces propriétés, elles peuvent même les démontrer; il y a, par contre, des propriétés non démontrables dans T, et qui n’ont pas le moindre rapport avec T... De plus, le théorème ne dit rien sur la science en général, et encore moins sur la pensée!

Il est certain que les théorèmes d’incomplétude ont un sens général qui transcende la formulation technique précise de ces énoncés, mais ce n’est pas n’importe quoi! On pourrait dire que les théorèmes parlent de la pensée mécanique et de ses limites. Pourquoi ne pas formuler le résultat de la manière suivante: Il y a des choses qui ne sont pas du ressort du mécanique .

2. Le calcul des séquents

L’ontologie hilbertienne se fondait sur les énoncés 刺⁰¹. À bien des égards, la classe duale ( ⁰¹) a un bien meilleur comportement; par exemple, tout énoncé ⁰¹ vrai est prouvable par des méthodes élémentaires. À partir de cela, l’analogue du programme de Hilbert pour les énoncés ⁰¹ devient démontrable pour les théories courantes; mais la démonstration n’est pas élémentaire! ⁰¹ est la complexité logique de la démonstrabilité dans les systèmes de logique usuelle (finitaire). Les travaux de Gentzen, vers 1935, ont permis de démontrer un principe de pureté des méthodes pour le calcul des prédicats, c’est-à-dire la logique pure, sans axiomes. En quelque sorte, ce que Hilbert voulait faire avec les mathématiques élémentaires, Gentzen le réalisa dans le cadre du calcul des prédicats.

Système LK

Dans ce qui suit, L est un langage du premier ordre arbitraire. Un séquent est une expression formelle 臨 塞 , où 臨 et sont des suites finies d’énoncés de L. L’interprétation intuitive de A¹, ..., Aⁿ 塞 B¹, ..., B^m , c’est que la conjonction des Aⁱ implique la disjonction des B^j . En particulier, 塞 A veut dire A, et A 塞 veut dire 囹 A; quant au séquent vide 塞, il signifie l’absurdité. Dans les systèmes séquentiels, la cohérence sera toujours interprétée par la non-prouvabilité de 塞.

Dans la formulation qui suit du calcul des séquents LK, on utilise la virgule pour dénoter la mise bout à bout (concaténation) de suites, par exemple 臨, 炙; on utilise 臨, A au lieu de 臨,A.

Les règles représentées dans le tableau ci-après sont divisées en quatre groupes; mais elles sont d’importance inégale. En particulier, les règles structurelles sont de peu d’intérêt; il convient cependant de ne pas mépriser l’importance des règles de contraction. Dans les groupes II et III, les règles sont divisées en droites et gauches: pour toutes ces règles (sauf l’échange), on a une «formule principale »: il s’agit de la formule écrite explicitement en conclusion; sa localisation par rapport à 塞 détermine le caractère gauche ou droit de la règle; dans la règle de coupure, A est la formule de coupure.

Théorème de complétude . Le séquent 臨 塞 est vrai dans tout modèle de L si et seulement s’il est démontrable dans LK.

En particulier, si on se restreint aux séquents de la forme 塞 A, LK est équivalent au calcul des prédicats.

Théorème d’élimination des coupures (Hauptsatz de Gentzen). Dans LK, la règle de coupure (C) est inutile, autrement dit tout théorème de LK est démontrable sans coupures. La démonstration de ce résultat, assez longue et délicate, consiste à remplacer toute coupure de formule principale A par de nombreuses coupures dont les formules de coupure sont des sous-formules (voir leur définition plus bas) strictes de A.

Donnons quelques exemples:

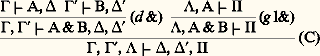est remplacée par:

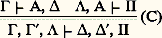(la double barre indique que, en plus de la coupure, on a utilisé un certain nombre de règles structurelles).

De la même manière,

devient:

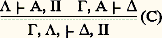et on remplace enfin:

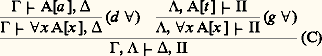par: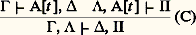

La démonstration de 臨 塞 A[t ], est obtenue en remplaçant a par t dans la démonstration de 臨 塞 A[a ], . Dans la pratique, tout est rendu beaucoup plus compliqué par la règle de contraction, mais l’idée essentielle est exprimée dans les exemples donnés ci-dessus.

Le Hauptsatz a pour corollaire la propriété de la sous-formule. Par définition, une sous-formule de A est soit A elle-même, soit:

– dans le cas où A est 囹B, toute sous-formule de B,

– dans le cas où A est B 鈴 C, B & C, BC, toute sous-formule de B et/ou de C,

– dans le cas où A est 葉x B[x ], 說x B[x ], toute sous-formule des formules B[t ], t étant un terme quelconque.

Théorème. La «propriété de la sous-formule» s’exprime sous la forme du résultat suivant, dû à Gentzen: Si 臨 塞 est démontable dans LK, il a une démonstration n’utilisant que des séquents formés de sous-formules des formules de 臨 塞 .

Démonstration: par le Hauptsatz , il suffit de vérifier la propriété pour les démonstrations sans coupures; pour ces dernières, remarquons que, dans les groupes (II) et (III), les séquents en prémisse sont formés de sous-formules du séquent conclusion: le théorème est donc une conséquence de la transitivité de la notion de sous-formule.

Gentzen a donc réussi à prouver un résultat qui est un véritable principe de pureté des méthodes pour le calcul des prédicats: les formules apparaissant dans une démonstration sans coupures de 臨 塞 sont parfaitement (aux substitutions de termes près) prévisibles. Il importe, cependant, de dire nettement que le calcul sans coupures, s’il est beaucoup plus intéressant à étudier que le calcul avec coupures, ne correspond pas du tout à la pratique; en effet, la règle de coupure correspond à un passage du général au particulier. En éliminant les coupures, on élimine tous les énoncés très généraux et, ce faisant, on obtient une démonstration longue (les démonstrations croissent exponentiellement quand on élimine les coupures) et bête (les «idées» de la démonstration sont contenues dans les propriétés générales!). Cela dit, il n’est pas sans intérêt de remplacer une démonstration avec coupures par une démonstration sans (ou du moins avec peu de) coupures: il est alors possible d’en extraire des informations de caractère effectif, typiquement des majorations (problèmes de bornes effectives). Parmi les utilisations possibles du Hauptsatz , mentionnons la possibilité d’en déduire une démonstration syntaxique du lemme d’interpolation (cf. théorie des MODÈLES). On peut aussi utiliser le Hauptsatz pour donner des démonstrations de cohérence: par exemple, considérons l’arithmétique récursive primitive ARP, qui est un système contenant des équations de définition pour toutes les fonctions récursives primitives et le principe d’induction (récurrence) sur les énoncés sans quantificateurs. Par le Hauptsatz , toute contradiction dans le système peut être ramenée à une contradiction dans sa partie purement équationnelle. La cohérence du système équationnel ne peut pas être établie dans le système lui-même, mais elle n’est pas vraiment douteuse. Par contre, la cohérence relative du système avec quantificateurs par rapport au système équationnel fait problème: cela montre que l’impossibilité prévue par le deuxième théorème d’incomplétude, si elle est bien absolue, n’est pas nécessairement due à des phénomènes très profonds.

Mentionnons au passage une variante importante du calcul des séquents, la déduction naturelle ; c’est un système à peu près équivalent au calcul des séquents, mais plutôt tourné vers l’intuitionnisme. Cette formulation a surtout été étudiée par Prawitz.

Un autre corollaire du Hauptsatz de Gentzen est le théorème du séquent médian pour les énoncés en forme prénexe. Ici, nous préférerons un résultat proche, dû à Jacques Herbrand, antérieur aux travaux de Gentzen: pour fixer les idées, prenons un énoncé prénexe 說x 葉y 說z 葉t B[x , y , z , t ], avec B sans quantificateurs; soit f et g de nouvelles lettres de fonctions, à une et deux places; si face="EU Domacr" 龜 = t ¹, ..., t ⁿ et face="EU Domacr" 契 = u ¹, ..., u ⁿ sont deux suites de termes de même longueur, utilisant f et g , on définit:

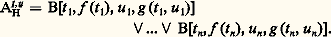Théorème «fondamental» de Herbrand (1930). Si A est démontrable dans le calcul des prédicats, alors on peut trouver deux suites finies face="EU Domacr" 龜 et face="EU Domacr" 契 telles que A^H face="EU Domacr" size=1^{龜 ,} face="EU Domacr" size=1^契 soit une tautologie.

La démonstration peut être obtenue à partir du Hauptsatz , sous sa forme de «séquent médian»; réciproquement, le théorème du séquent médian peut être déduit du théorème de Herbrand.

Le théorème de Herbrand est donc très proche du Hauptsatz ; c’est une formulation moins élégante, mais elle peut être utile dans certains cas. Il fournit, lui aussi, un principe de «pureté des méthodes».

Kreisel a donné une application remarquable de ces méthodes, à savoir le schéma de réflexion de l’arithmétique:

Théorème . Soit AP l’arithmétique de Peano de premier ordre, T un sous-système finiment axiomatisable de AP et A un énoncé arbitraire à une variable libre x ; soit enfin Thm^T (face=F0019 掠A 亮) l’énoncé de AP qui exprime que A est démontrable dans T. On a:

Pour la démonstration, on se ramène au cas où T est le calcul des prédicats; il s’agit de montrer, par induction sur une démonstration, que tout énoncé démontrable est vrai; or, c’est un résultat bien connu de Tarski, il n’y a pas de prédicat de vérité pour les énoncés de AP défini dans AP elle-même. Mais, par la propriété de la sous-formule (ou par le théorème de Herbrand), il est possible de travailler avec des prédicats de vérité bornés qui, eux, sont bien définissables... Le théorème est faux pour T = AP: si on prend A : face="EU Upmacr" 虜 = 路, on serait en contradiction avec le second théorème d’incomplétude.

La question de l’extension du Hauptsatz à des systèmes plus forts que le calcul des prédicats est une question essentielle en théorie de la démonstration. Parmi les généralisations proposées, la plus connue est la «conjecture fondamentale» formulée par Takeuti en 1953 pour un calcul G¹LC: il s’agit d’une expression purement logique de l’arithmétique du second ordre AP² (on dit encore l’analyse). Dans G¹LC, on admet des variables X, Y, Z pour des ensembles d’entiers, ainsi que des termes d’abstractionx B[x ], pour l’ensemble des x tels que B[x ]; dans A[X] on peut substituer le termex B[x ] pour X, puis remplacer tous les atomes t 捻x B[x ] par des formules B[t ]: le résultat est noté A[T]; les règles logiques pour le quantificateur 葉X sont: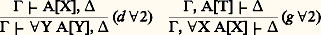

Dans (d 葉2), X n’est pas libre dans 臨, ; dans (g 葉2), T est un terme d’abstraction arbitraire; on écrirait des règles symétriques pour 說X. Le système, bien que purement logique, démontre le schéma de compréhension 說X 葉x (x 捻 X 良轢 A[x ]), où A est un énoncé quelconque ne contenant pas X. La conjecture de Takeuti est la généralisation du Hauptsatz à ce système.

En 1960, Schütte donnait un équivalent sémantique à la conjecture et Tait la démontrait sous cette forme en 1965. Mais la forme syntaxique de la conjecture appelait une approche non sémantique. La question était de savoir si, en remplaçant systématiquement les coupures:

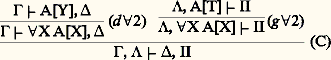par des coupures de la forme:

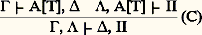on obtenait finalement une démonstration sans coupures. Une réponse affirmative fut apportée en 1970 par Jean-Yves Girard.

En fait, la conjecture de Takeuti est l’exemple même de ces questions saturées d’intentions philosophiques, mais dont le contenu mathématique réel est assez mince: un écueil que la théorie de la démonstration ne sait pas toujours éviter. On a pu montrer que, dans les cas vraiment intéressants, il n’y avait pas de différence sensible entre démonstration avec ou sans coupures au sens de Takeuti; d’ailleurs, le système ne vérifie aucune propriété de la sous-formule acceptable. Ce qui reste de cette conjecture, c’est l’aspect sémantique, valable pour tous les calculs sans coupures: on peut interpréter les règles sans coupures dans des modèles à trois valeurs (vrai, faux, indéterminé) et 臨 塞 se lit: de la vérité de 臨 on conclut à la non-fausseté de ; les règles sans coupures préservent cette interprétation. Par contre, la coupure dit que: Si A est non faux, il est vrai; écrire la coupure pour A arbitraire veut bien dire que l’on se restreint à des modèles binaires, où la valeur indéterminée n’est pas prise. Cet aspect sémantique, appliqué à d’autres systèmes, reste très actuel.

3. L’ordinal size=5﨎⁰ et la size=5諸-logique

À plusieurs reprises dans les années trente, Gentzen allait donner des démonstrations de cohérence pour l’arithmétique de Peano AP. Pour obtenir de tels résultats, il était nécessaire, par le second théorème d’incomplétude, de se servir de méthodes extérieures à l’arithmétique. Gentzen utilisa comme méthode l’induction transfinie jusqu’à 﨎⁰, où 﨎⁰ est défini comme le suprémum des ordinaux 諸ⁿ , avec 諸⁰ = 1, 諸ⁿ⁺¹ = 諸 size=1^諸n ). Dans les années cinquante, Schütte allait donner une version plus accessible de ces mêmes résultats: essentiellement, l’arithmétique de Peano est obtenue à partir du calcul des prédicats en ajoutant le schéma d’axiomes d’induction:

où A est un énoncé arbitraire. Schütte introduit une logique, la 諸-logique, où ce schéma est logiquement démontrable: les règles pour 葉 sont: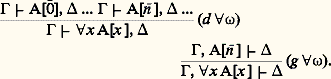

On écrit des règles symétriques pour le quantificateur 說. La principale nouveauté de ces règles, c’est leur caractère infinitaire: la règle (d 葉 諸) nécessite une infinité de prémisses. Dans ces conditions, est-il encore possible de parler d’aspect syntaxique? oui; car, bien qu’infinies, ces démonstrations (qui ne sont rien d’autre que des arbres dont les nœuds sont occupés par des séquents) peuvent être représentées par des fonctions récursives dans les bons cas, d’où un concept de 諸-démonstration récursive. Par contre, l’ensemble des indices (ou codes) de 諸-démonstrations récursives est de complexité logique 刺¹¹.

Le schéma d’induction devient démontrable dans la 諸-logique; c’est, en fait, un cas particulier du théorème suivant, dû à Orey:

Théorème d’ 諸-complétude. 臨 塞 est vrai dans tout 諸-modèle (modèle dont le domaine est exactement N et où 虜 et S sont interprétés de façon standard) si et seulement s’il y a une 諸-démonstration récursive de 臨 塞 .

Dans la pratique, on se contentera de construire explicitement une démonstration d’un axiome d’induction à l’aide de (d 葉 諸). On a le Hauptsatz suivant, dû à Schütte:

Théorème. La 諸-logique vérifie l’éliminition des coupures.

La démonstration consiste, pour l’essentiel, à remplacer toute coupure:

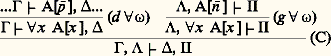par: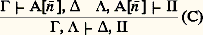

Si l’on part d’une démonstration dans AP, alors, on obtient une démonstration avec coupures dans la 諸-logique en utilisant la démonstration des axiomes d’induction, puis, par élimination des coupures, une démonstration sans coupures du même séquent en 諸-logique. On peut calculer la hauteur d’une telle démonstration (c’est-à-dire l’ordinal qui mesure la hauteur de l’arbre de la démonstration): elle est strictement inférieure à 﨎⁰. En particulier, le principe d’induction transfinie jusqu’à l’ordinal récursif 﨎⁰ nous permettra de démontrer que l’arithmétique est non contradictoire... Plus précisément et c’est un résultat dû à Mints, on peut démontrer le théorème d’élimination des coupures pour la 諸-logique, de telle manière que l’on ait la borne effective 﨎⁰ pour toutes les démonstrations issues de l’arithmétique (mais rien ne dit que les arbres de démonstration ainsi obtenus sont bien fondés) et de telle manière que le tout se fasse élémentairement.

Donc, par une induction jusqu’à 﨎⁰, on montre facilement qu’il ne saurait y avoir de démonstration du séquent 塞. Ici encore, on peut poser la question «N’y a-t-il pas surcharge d’intentions?» Après tout (Kreisel dixit ), «les doutes quant à la cohérence sont infiniment plus douteux que la cohérence elle-même». On rappellera le mot d’un mathématicien français: «Gentzen est le type qui a prouvé la cohérence de l’arithmétique, c’est-à-dire de l’induction jusqu’à 諸, au moyen de l’induction jusqu’à 﨎⁰». En fait, il est facile de remarquer que, si d’un côté on a l’induction jusqu’à 諸, c’est sur des énoncés arbitraires, alors que l’induction jusqu’à 﨎⁰ utilisée par Gentzen se fait uniquement sur des énoncés sans quantificateurs. Autrement dit, un quantificateur égale une exponentielle ordinale. Le résultat de Gentzen n’est donc pas aussi stupide que certains le laissent entendre.

La découverte de la relation entre 﨎⁰ et AP induisit les théoriciens de la démonstration à parler de l’«ordinal» de AP et à rechercher les ordinaux d’autres théories. En particulier, les travaux de Takeuti (1967), repris et simplifiés par Pohlers (1975), allaient permettre d’analyser, toujours au moyen de la 諸-règle, les théories de définitions inductives ou, de manière équivalente, le schéma de compréhension 刺¹¹. Par exemple pour le système de définitions inductives le plus simple, ID¹, l’ordinal associé est un ordinal 兀⁰, appelé encore «ordinal de Howard». Mais, alors que le Hauptsatz pour la 諸-logique est complet, le calcul des séquents de Pohlers et ses variantes (Buchholz) ne vérifie l’élimination des coupures que pour des séquents de forme très particulière.

En fait, l’idée même d’ordinal d’une théorie est critiquable. L’assignement de 﨎⁰ à AP par Gentzen ne doit pas faire oublier la possibilité de relations de nature différente de AP avec d’autres ordinaux. Par exemple, il est possible de définir, pourvu que l’on dispose, pour chaque ordinal limite considéré, d’une suite fondamentale convergeant vers cet ordinal, des hiérarchies:

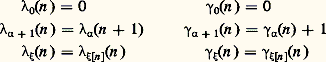Dans le dernier cas, 﨡 est limite, de suite fondamentale 﨡[n ].

Un corollaire du Hauptsatz pour la 諸-logique est que, si on peut prouver dans AP que la fonction récursive f est totale, alors f est majorée par un size=1^見, pour un 見 strictement inférieur à 﨎⁰.

En 1975, Girard établit le résultat suivant:

Théorème (comparaison de hiérarchies):

Cela montre que, si on se pose la même question en termes de hiérarchie 塚 (hiérarchie lente, ou mieux: hiérarchie ponctuelle), il faut aller jusqu’à 兀⁰. Il est donc hâtif de réduire l’aspect ordinal de AP au seul 﨎⁰.

Cela dit, revenons à la question de l’intérêt du résultat de Gentzen. Kreisel a proposé d’extraire, par-delà les déclarations philosophiques douteuses, un contenu positif aux résultats de Gentzen, à savoir des résultats mathématiques indépendants de toute considération «fumeuse». Ainsi, il a énoncé le résultat suivant:

Théorème. Si un énoncé 葉x A[x ], avec A sans quantificateurs, est démontrable dans AP, alors on peut aussi l’établir en utilisant uniquement l’induction transfinie jusqu’à un ordinal strictement inférieur à 﨎⁰ et sur des énoncés sans quantificateurs.

Un tel résultat est, en quelque sorte, un principe de pureté des méthodes pour l’arithmétique et montre que, certainement, une partie importante du programme de Hilbert peut être préservée. On peut se ramener à des méthodes élémentaires, en donnant un sens élargi à «élémentaire»; ici, par exemple, on admettra l’induction transfinie jusqu’à 﨎⁰ comme un nouveau principe élémentaire, pourvu que cette induction se fasse sans quantificateurs.

Par contre, de tels principes généralisés ne peuvent pas être engendrés mécaniquement (comment sait-on que 﨎⁰ est un bon ordre? sûrement pas par une vérification de type mécanique) et le côté mécanique du programme de Hilbert (et c’est un aspect essentiel) reste caduc.

Les interprétations fonctionnelles sont un autre cas d’utilisation de l’esprit de la 諸-logique pour le traitement de l’arithmétique. Prenons pour exemple l’énoncé A considéré plus haut pour le théorème de Herbrand: Kreisel établit, en 1952, le résultat suivant, dit no counterexample interpretation :

Théorème. L’énoncé A est vrai, dans la structure N des entiers, si et seulement si on peut trouver des fonctionnelles récursives continues 淋 et 切 telles que: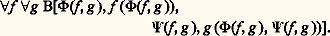

Ce résultat généralise le théorème de Herbrand à la 諸-logique, comme le Hauptsatz de Schütte généralise le théorème de Gentzen.

L’interprétation fonctionnelle de Gödel (1958) associe à tout énoncé de l’arithmétique (ici intuitionniste HA) un énoncé de la forme 葉x size=1^靖 說y size=1^精 A[x , y ], où x size=1^靖 et y size=1^精 sont des variables variant parmi des fonctionnelles de type fini et où A est sans quantificateurs. Gödel a introduit un système T pour les fonctionnelles de type fini, dont le gros morceau est l’opérateur R de récursion primitive de type fini qui vérifie les équations: R(a , b , 拏 ) = a ; R(a , b , S(c )) = b (R(a , b , c ), c ). Le fait que tous les termes clos de type 晴 (type des entiers) soient calculables au moyen des équations de définition n’est pas démontrable dans l’arithmétique elle-même. En effet, ce fait permet de donner un modèle à T formé de terme clos, et on peut alors déduire la cohérence de HA (ou PA) du résultat suivant:

Théorème (interprétation de Gödel). Si A est un théorème de HA et si son interprétation est 葉x size=1^靖 說y size=1^精 A [x , y ], alors on peut trouver un terme t de T de type 靖 tel que T 塞 A [t , y ].

L’interprétation de Gödel fournit en théorie un instrument de tout premier ordre pour l’analyse de la démonstrabilité en arithmétique. Malheureusement, l’interprétation elle-même est beaucoup trop complexe. Mentionnons, pour mémoire, l’existence d’extensions de l’interprétation de Gödel au second ordre faites par Spector en 1961 et par Girard en 1970.

4. La logique size=5刺¹²

L’extension des résultats obtenus par Takeuti, Pohlers, Buchholz... pour le schéma de compréhension 刺¹¹ à des systèmes plus forts nécessite de remplacer la 諸-logique par des logiques correspondant à de plus grandes complexités logiques, 刺²¹ et plus généralement 刺¹ⁿ . Le problème de la B -règle, posé par Mostowski est le suivant: Caractériser les énoncés qui sont vrais dans tout modèle dans lequel les objets d’un type distingué 行 sont interprétés par un ordinal 見 et où la relation 諒 distinguée entre objets de type 行 est interprétée par l’ordre de 見 (B -modèles). Une réponse simple est donnée par: pour tout 見, nous avons une démonstration au moyen de la 見-règle, qui est l’analogue de la 諸-règle, obtenu en remplaçant 諸 par 見. Cela dit, une famille (P size=1^見) de 見-démonstrations indexées par tous les ordinaux ne constitue pas spécialement un objet syntaxique! On définit la catégorie ON des ordinaux en prenant pour morphismes les ensembles I( 見, 廓) d’applications strictement croissantes de 見 vers 廓. Si P est une 廓-démonstration, on peut, dans certaines conditions, définir, si f 捻 I( 見, 廓), une 見-démonstration f ^-1(P). Si on demande que la famille (P size=1^見) soit telle que f ^-1(P size=1^廓) = P size=1^見, alors cette famille est appelée une B -démonstration. Une B- démonstration apparaît, en fait, comme un foncteur de la catégorie ON dans une catégorie DEM de démonstrations et on vérifie qu’un tel foncteur préserve les limites directes (c’est-à-dire inductives filtrantes) et les produits fibrés. En particulier, la donnée de la famille (Pⁿ ), pour n fini, détermine uniquement (par unicité du prolongement par limites directes) la famille (P size=1^見). Il devient alors possible de parler de B -démonstration récursive, autrement dit nous avons un concept syntaxique. (Mais l’ensemble des indices de B -démonstrations est 刺¹².) Et Girard a pu établir en 1978 la B -complétude:

Théorème. 臨 塞 est vrai dans tout B -modèle si et seulement s’il y a une B -démonstration récursive de ce séquent.

Un concept proche est celui de dilatateur : un dilatateur est un foncteur de ON dans ON préservant les limites directes et les produits fibrés. La plupart des fonctions ordinales (x + 1, 諸^x , la hiérarchie de Veblen) sont, en fait, des dilatateurs. Comme un dilatateur est déterminé par sa restriction à la souscatégorie des entiers, il peut être récursif. Le résultat élémentaire sur les dilatateurs est le théorème de forme normale:

Théorème. Si l’on a z 麗 F(x ), alors on peut écrire z = (z ⁰; x ⁰, ..., x ^n-1 ; x )^F, ce qui signifie que:

(1) z = F(f ) (z ⁰), si f 捻 I(n , x ) est défini par f (0) = x ⁰, ..., f (n 漣 1) = x ^n-1 ,

(2) n est minimum tel que (1) soit vrai.

Si (1) et (2) sont vérifiés, alors la forme normale est unique.

Ce résultat généralise le théorème de forme normale de Cantor.

En utilisant une combinaison de B -logique et de dilatateurs, il est possible de donner une nouvelle démonstration de l’élimination des coupures pour l’arithmétique, ainsi que les définitions inductives. Par rapport aux résultats existant auparavant, on a ici un théorème complet d’élimination des coupures, ainsi qu’une propriété de sous-formule; on a surtout son corollaire, également dû à Girard (1979):

Théorème (majoration des fonctions 諸^1CK-récursives). Si f est une fonction 諸^1CK récursive, alors il existe un dilatateur récursif D tel que 葉x ( 諸 諒x 麗 諸^1CKF(x ) 麗 D(x )).

Ce résultat ramène, en quelque sorte, la 諸^1CK-récursion à la récursivité habituelle. L’élimination des coupures utilise un principe d’induction sur les dilatateurs qui a ceci de particulier que la relation d’ordre entre dilatateurs est telle que l’ensemble des prédécesseurs de F est une classe bien ordonnée de type d’ordre F(On ). Pour l’arithmétique, l’élimination des coupures donne l’ordinal de Howard 兀⁰.

Ces méthodes fonctorielles s’étendent et se généralisent. En particulier, en utilisant les concepts 刺¹³, analogues des concepts de la logique 刺¹², il a été possible de mener à bien l’analyse ordinale du schéma de compréhension 刺¹² (Girard, 1981) et, vraisemblablement, cette méthode se généralise au schéma de compréhension 刺¹ⁿ . Le principal problème est de trouver des applications à tous ces résultats.

Encyclopédie Universelle. 2012.